On Variance as an Explanation for Dominance in Certain Fields
I found myself recently reading a Reddit conversation about electrical outlets, specifically comparing outlets in the US vs the UK. This... isn't an area that I have a deep and abiding interest in, but I found the discussion about safety features interesting. The comments were mostly discussing how UK outlets have a number of safety features not present in the US (fuses, ground must engage before the outlet), and how you would expect a higher rate of electrical injuries in the US as a result. (Of course with GFCI/AFCI style breakers and outlets now being the norm, the US outlet design may not be as unsafe as it appears.)
One of the statistics brought up was a comprehensive report from the United States Consumer Product Safety Commission: [./Electrocutions-2011-to-2020.pdf](Electrocutions Associated With Consumer Products: 2011-2020). This showed a much higher rate of electrocution in the US vs the UK. Initially commenters felt like this reinforced the belief in the superior safety of UK systems. But then someone pointed out that the US report was a bit broader than the UK report. Specifically, they pointed out that a large number of electrocutions were due to "Fractal wood burning". From the report:
Fractal wood burningAlso referred to as Lichtenberg, fractal wood burning is an embellishing technique that uses high voltage electric current to burn patterns on wood. emerged as a major source of electrocutions during this reporting period. It often involved tampering with microwaves and other devices to produce the electricity the practice requires. A third of the reports received from 2018-2020 mentioned wood burning explicitly, and other reports may indicate wood burning indirectly.
Then this perhaps unsurprising comment struck me:
There were nearly nine times as many estimated consumer product-related electrocutions to males than to females over the years 2011 through 2020.
So a large portion of the injuries in the US were due to people (men) modifying a microwave to burn wood. It's fair to say this isn't the outlets fault anymore. For some reason this made me think about statistical distributions. Clearly most men don't injure themselves trying to burn patterns into wood. But there's an outlier set that really does. What if the distribution of "likelihood to electrocute oneself trying to burn patterns into wood" actually had the same mean for men and women, but men had higher variance? Would that be enough to explain our propensity for self-injury?
On the Distribution of "Playing with Fire"
If we make 2 normal distributions (let's assume there's a lot of independent factors that combine to make you interested in wood patterning) and slightly perturb the standard deviation, we see as expected a big swing on the tail:
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats
def plot_normal(mean, std, label):
x = np.linspace(mean-10*std, mean+10*std, 1000) * 200e6
p = stats.norm.pdf(x, mean, std)
sns.lineplot(x=x, y=p, label=label)
plot_normal(0, 1, 'male')
plot_normal(0, 0.9, 'female')
plt.xlim(5, 10)
plt.ylim(0, 1e-6)
plt.legend()
plt.show()
It doesn't take much of a change in the variance to show a huge delta in the tail - the group of people who bring to bear their full resources to hurting themselves with electricity:
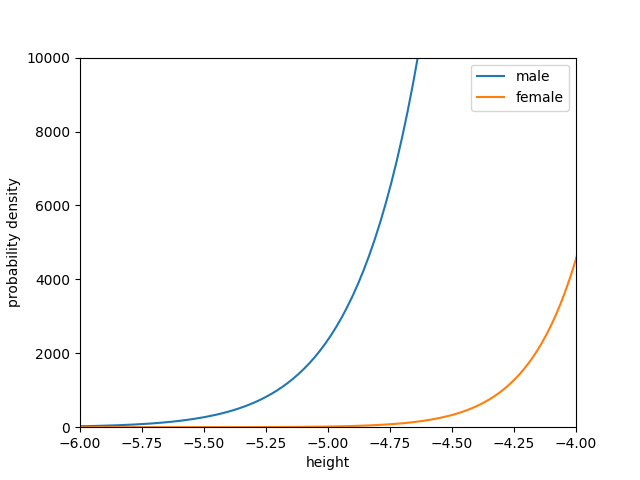
If we look at the ratio of the distributions, this becomes even more obvious:
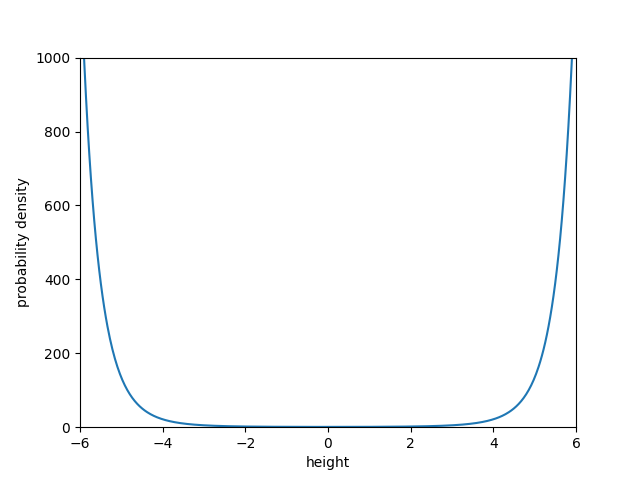
This is of course all just handwaving and tongue in cheek. It's difficult to assign a clear value to such an idiosyncratic variable, but it's fun to imagine proxies (intelligence, risk tolerance, impulsivity) which could result in a similar outcome.
On How we Perceive Distributions
As I was thinking in this direction, I started to wonder if we, societally, might be mis-characterizing distributions by focusing excessively on outliers, or just the mean, instead of characterizing the entire distribution of groups. For example the structure of athletics and how we play games has a tendency to exacerbate differences - if I'm even 5% slower than the best swimmer/runner/etc in the world, I might not even make a college team, much less the Olympics. A sport like tennis might require excellence on multiple dimensions - being a tiny bit worse on each might be the difference between being an all-time great and never making it. It's not that it's bad to care about who the best player or team is, but the structure of the competition tends to "spread out" the outliers and make them seem even more unreal.
Unsurprisingly, I'm not the first person to think about this. A 2021 study from the University of Washington saw an undue focus on the mean of distributionsI'm not sure about the quality of this study, I see too many rather simple pictures given the claims, but instead of saying "this is a real phenomenon", let's just say "other people have thought about this". .
If you toy around with this idea, you start to see how it could explain all sorts of weird behavior. As an American, I don't feel that we're especially well educated on average compared to many other countries (and certainly you can look at any number of school tests to see evidence for this). It feels hard to understand how the US can be so wealthy despite this discrepancy. One explanation is simply hangover from post-WWII US dominance, but what if the US also has extremely high variance in intellgence or rather "ability to make money"? You only need a few companies like Apple or Nvidia to make up for a lot of low productivity. And you only need a small number of bright people to drive these forward.
Of course, all these observations are likely completely wrong! That said, it's kind of fun to hold the possibility of variance in your mind as an explanation instead of assuming a systemic bias.